Model family
Our library consists of a collection of rheological elements or modules that can be arranged in different forms.
Some modules have to be used in combination with others in order to provide physical sense (for example, modules representing viscosity or damage).
Five basic categories are distinguished: (i) elementary linear response, (ii) elementary nonlinear response, (iii) complementary modules, (iv) classical solids and (v) combined advanced material responses.
Some examples are shown below. (Notes: Not all possible combinations are listed. Curves in column "Behaviour overview" are only for illustrative purposes).
| Module name |
Behaviour overview |
Rheological representation |
Description |
| CSpringLangevin |


|
 |
This module describes a non-linear hyper-elastic material that follows the 3-chain and/or the 8-chain non-Gaussian network theory developed by Arruda-Boyce.
Reference: J. Mech. Phys. Solids, vol 41, issue 2, pp 389-412, 1993
|
| CDashpotPowerLaw |

|
 |
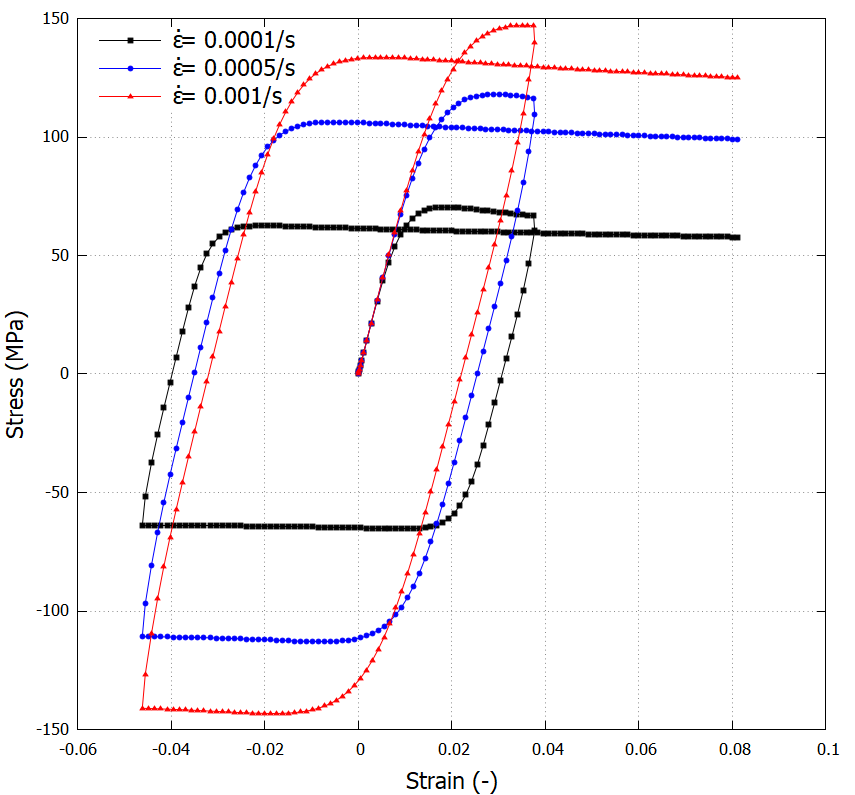
This module describes a commonly used rate-denpendent plasticity given by a Norton-Hoff type model (power-law).
The curve shown in "Behaviour overview" is obtained by connecting this module to a linear spring in series.
Reference: Proc. R. Soc. Lond. A. 348, 101-127, 1976
|
| CDashpotArgonBoyce |


|
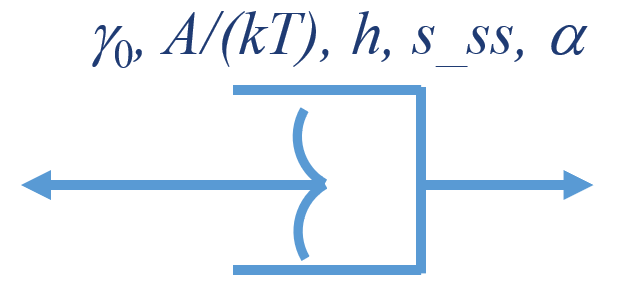 |
This module provides the response given by the physically-based model developed by Argon for predicting the rate- and temperature- dependent behavior of polymer below the glassy transition temperature.
The curve shown in "Behaviour overview" is obtained by connecting this module to a linear spring in series.
Reference: Mechanics of Materials 7 (1988) 15-33
|
| CDashpotGeneralized |

|
 |
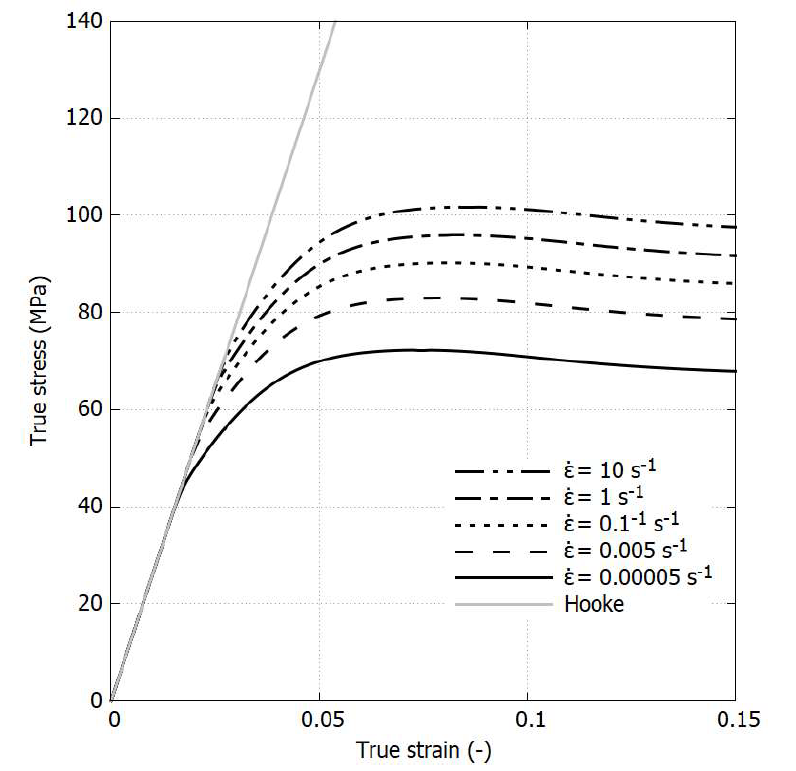
This module is an extension of the original Boyce-Parks-Argon model (rate- and temperature- dependent).
Enhanced with a phenomenological approach, the model is capable of capturing the pre- and post- yield behavior exhibited by some thermoplastics (PMMA, PC) and thermoset polymers (Epoxy).
The curve shown in "Behaviour overview" is obtained by connecting this module to a linear spring in series.
Reference: International Journal of Plasticity 62 (2014) 138-161
|
| CDashpotBergstromBoyce |

|
 |
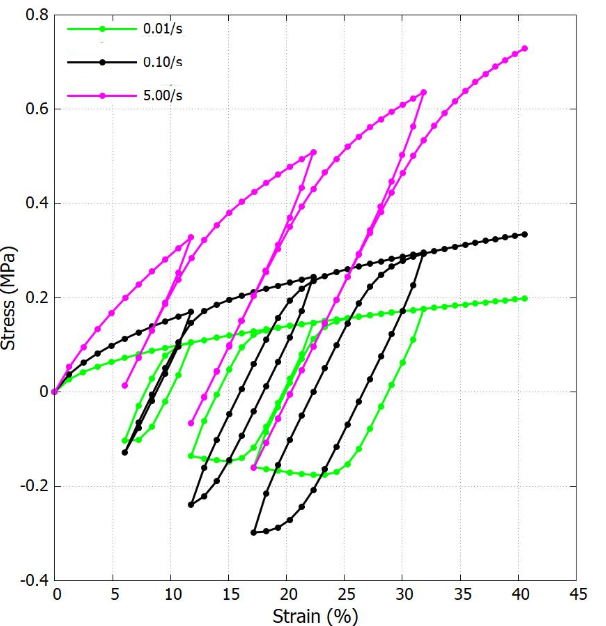
This module provides the nonlinear viscosity model developed by Bergstrom-Boyce.
By combining this module with hype-elastic modelus, this model is proved to properly capture the time-dependency response in Chloroprene rubbers (synthetic rubber also known with trade name 'Neoprene')
The curve shown in "Behaviour overview" is obtained by connecting this module to a linear spring in series.
Reference: J. Mech. Phys. Solids 46, 931-954, 1998
|
| CDamage |


|
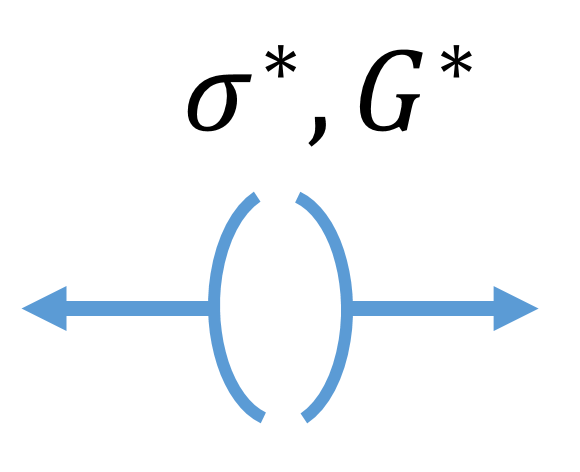 |
This module represents the softening part taking place in a damage process given by a traction-separation law.
Coupling between damage under tension and compression can be chosen.
Different criteria of damage initiation (principal strain, pressure-dependent parabolic function, stored energy, dilatation density energy or plastic strain) and different types of softening
(linear, bilinear, trilinear, superelliptic, exponential) are available.
Reference: Comp. Part B: Eng. 263 (2023) 110812 (study of energy absorption capability of vehicles' anti-intrusion bar made of thermoplastic composites)
|
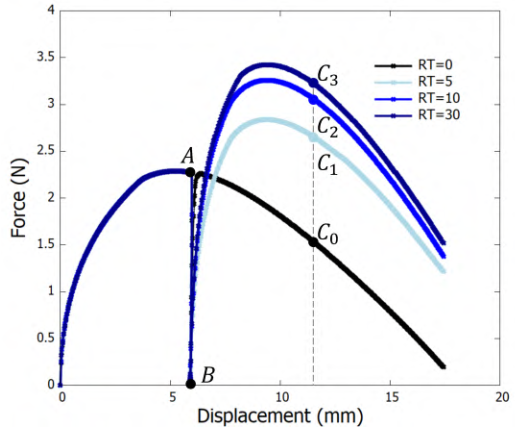
| CHealing |

|
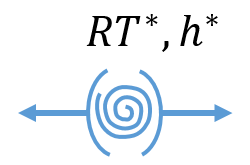 |
This module represents the healing mechanism in a damage process given either by a classical traction-separation law or a rate-dependent visco-damage model.
This healing model incorporates the effects of resting time (RT), loading rate and damage level (both instantaneous and accumulated) on the healing variable.
Reference: J. Int. Mech. Sciences 260 (2023) 108644 (multimaterial-aimed healing model incorporating dependency on resting time, strain rate and damage)
|
| Module name |
Behaviour overview |
Rheological representation |
Description |
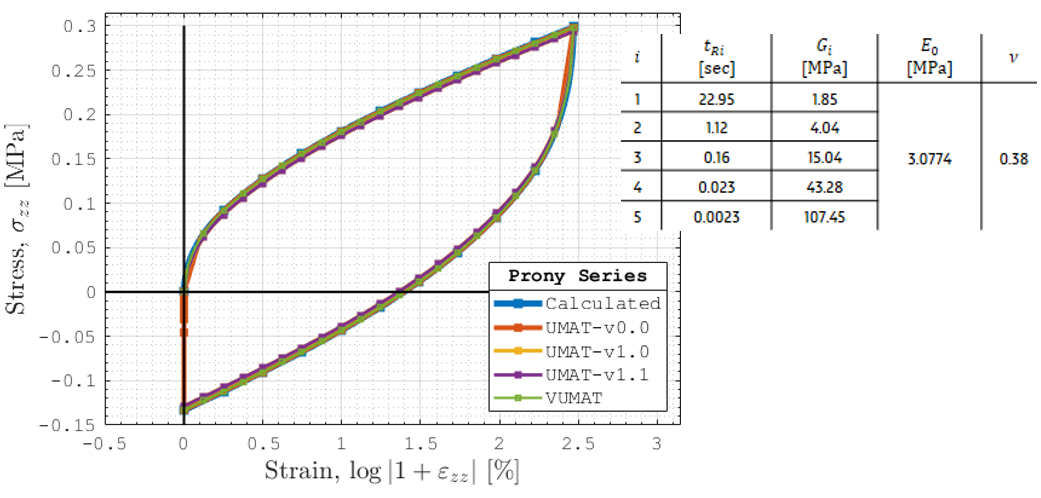
CPronyParallel
CSpringLinear
n x CMaxwell
|

|
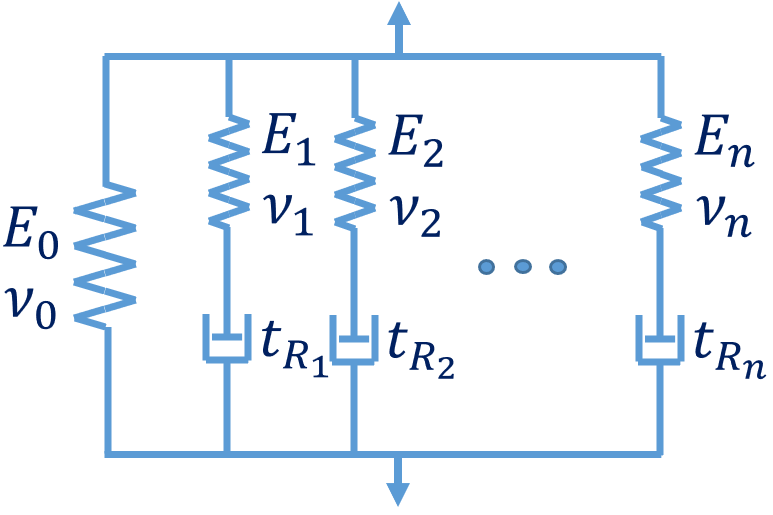 |
This combined module provides the response ruled by the so-called Generalized Maxwell model,
consisting of a linear elastic module connected in parallel to several parallel Maxwell branches.
This approach is commonly used to incorporate the rate dependency effect on the material stiffness.
Different viscosities were assigned to the dashpot of each Maxwell component to introduce different time scales.
Reference: Constr. Build. Mater. 283 (2021) 122725 (Application for the identification of viscoelastic parameters of asphalt matrix)
|
CPronySeries
CSpringLinear
n x CMaxwell
|


|
 |
This module is similar to the previous one except for the connection in series between the Maxwell branches and the linear elastic spring.
|
CMaxwellElastoPlastic
CElastoplastic
n x CMaxwell
|


|
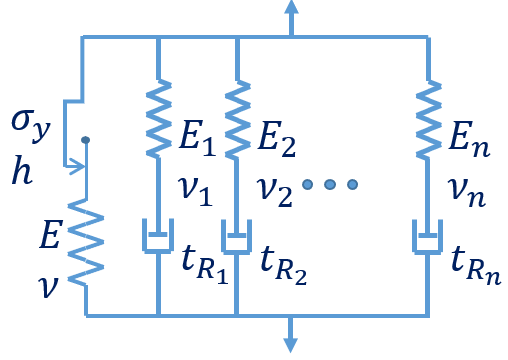 |
This module incorporates rate-independent plasticity into the Generalized Maxwell model.
|
CMaxwellElastoPlasticSeries
CElastoplastic
n x CMaxwell
|

|
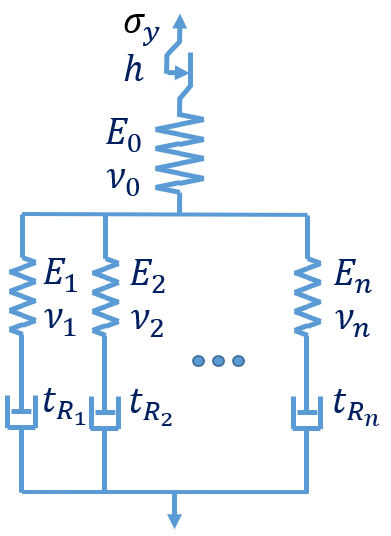 |
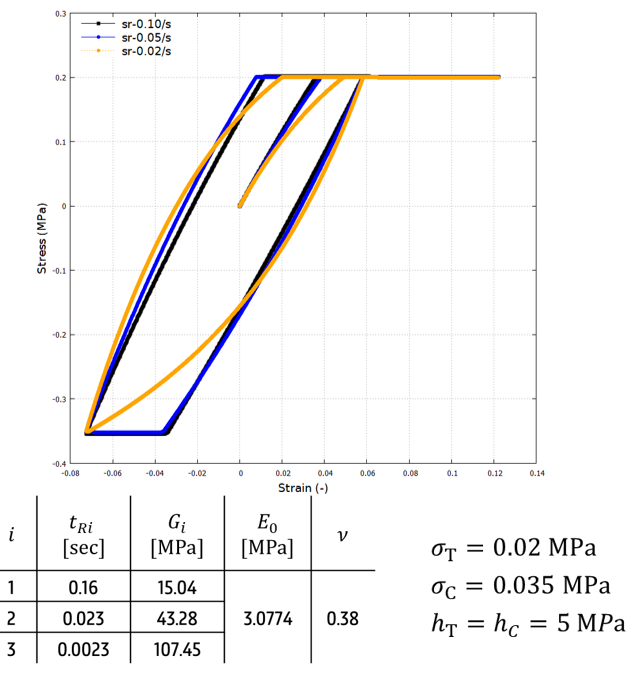
This module is obtained as a result of adding in series the classical elasto-plastic module to a collection or parallel-conected Maxwell branches.
|
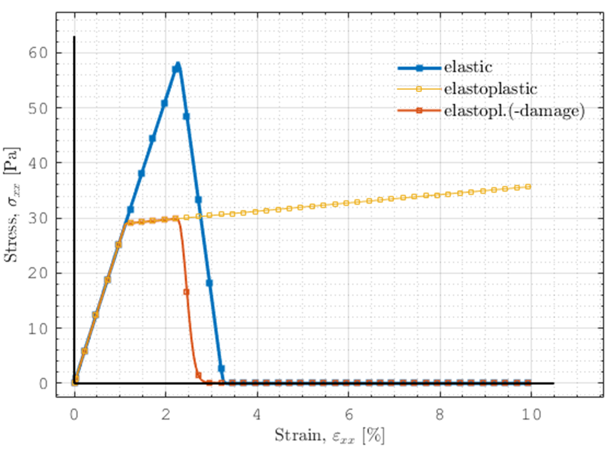
CElastoPlasticDamage
CElastoplastic
CDamage
|

|
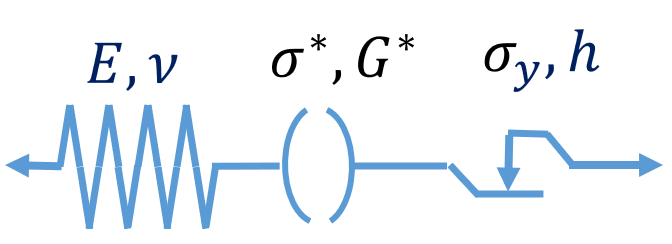 |
By adding damage in series, this combined module provides a handy representation of a rate-independent elasto-plastic-damageable solid.
|
CMaxwellDamage
CMaxwell
CDamage
|


|
 |
Connection between a classical Maxwell branch in series with a traction-separation-based damage module.
|
CMaxwellElastoPlasticDamage
CMaxwellElastoPlastic
CDamage
|


|
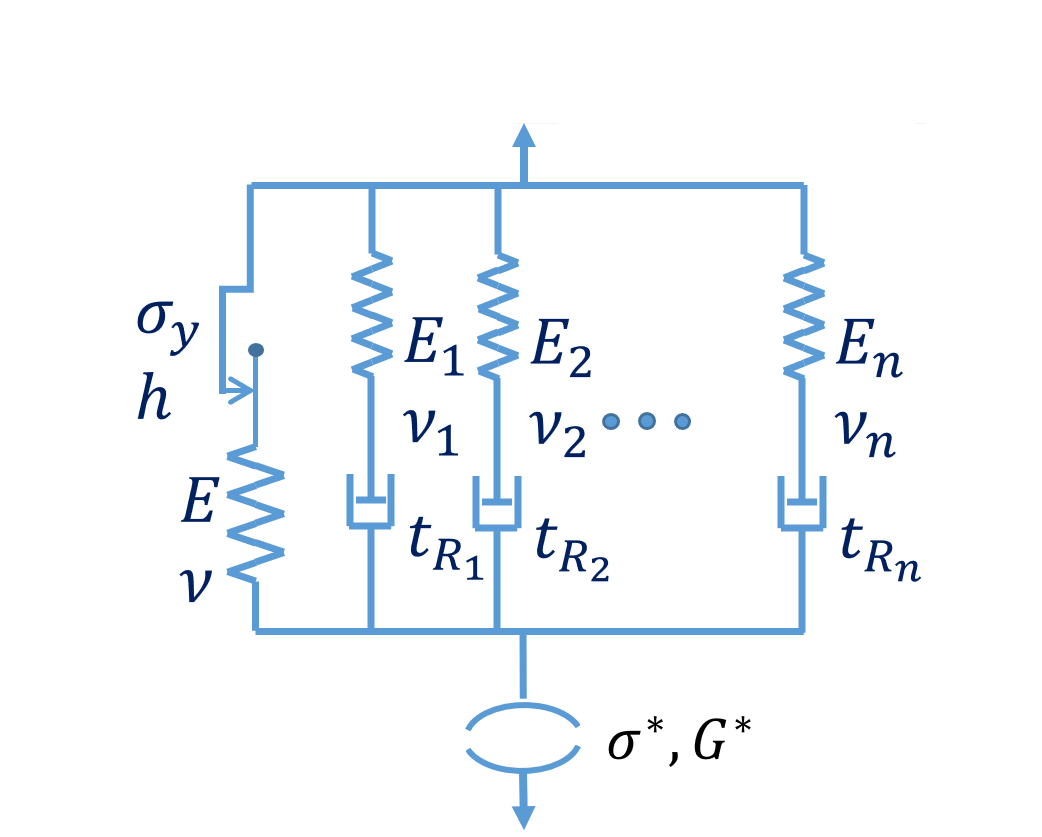 |
This module incorporates damage to the plastic-enriched version of the Generalized Maxwell model.
The resultant module is a visco-elastic-plastic-damageable solid.
By using a pressure-dependent yield criterion for the elasto-plastic component, this combined module makes it possible to describe asphaltic-based materials.
|
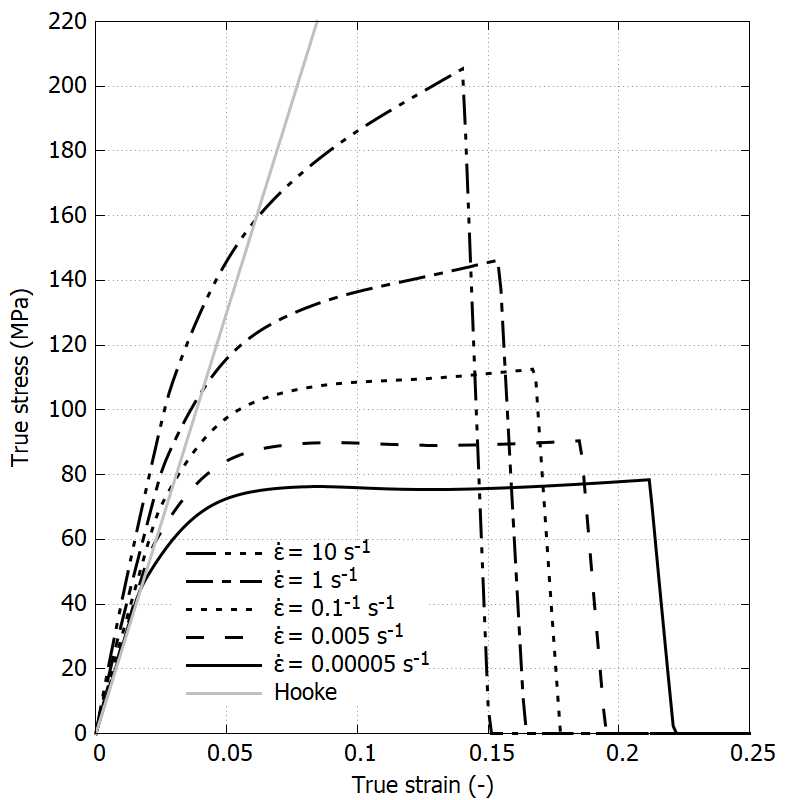
CMaxwellDashpotGeneralizedDamage
CSpringLinear
CMaxwell
CDashpotGeneralized
CDamage
|

|
 |
This module provides strain-rate dependency in stiffness and strength by combining non-linear visco-plasticity, the Generalized Maxwell model and energy-based damage.
This combined module makes it possible to describe the response of polymers.
Reference1: "Composite micro-scale model accounting for debonding, strain-rate dependence and damage under impact using an explicit finite element solver", 17th European Conference on Composite Materials
Reference2: "Modelling nonlinear material response of polymer matrices used in fiber-reinforced composites", Book chapter (ISBN: 9780128189856)
|
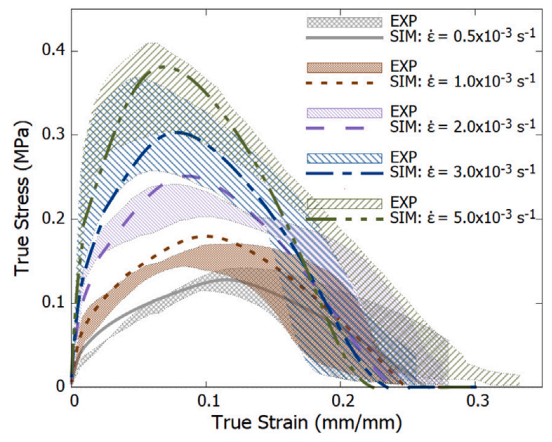
CAsphaltMatrix
CSpringLinear
CDashpotBergstromBoyce
CViscoDamage
|

|
 |
This module provides strain-rate dependency by combining liner-elastiticy, the non-linear Bergstrom-Boyce viscous dashpot and a rate-dependent version of the damage model derived from CDamage.
This combined module makes it possible to describe the response of the asphalt matrix.
Reference1: J. Int. Mech. Sciences 224 (2022) 107309 (rate- and pressure-dependent damageable model to capture compression–tension asymmetry in asphalt-based composites)
Reference2: 9th International Conference on Mechanics and Materials in Design (M2D2022), Funchal/Portugal, June 2022, ISBN:978-989-54756-3-6
Reference3: 10th International Conference on Mechanics and Materials in Design (M2D2024), Nagoya/Japan, September 2024, ISBN:TBD
|
CConstThermalDashpotGeneralized
CConstThermal
CSpringLinear
CDashpotGeneralized
CSpringLangevin
|


|
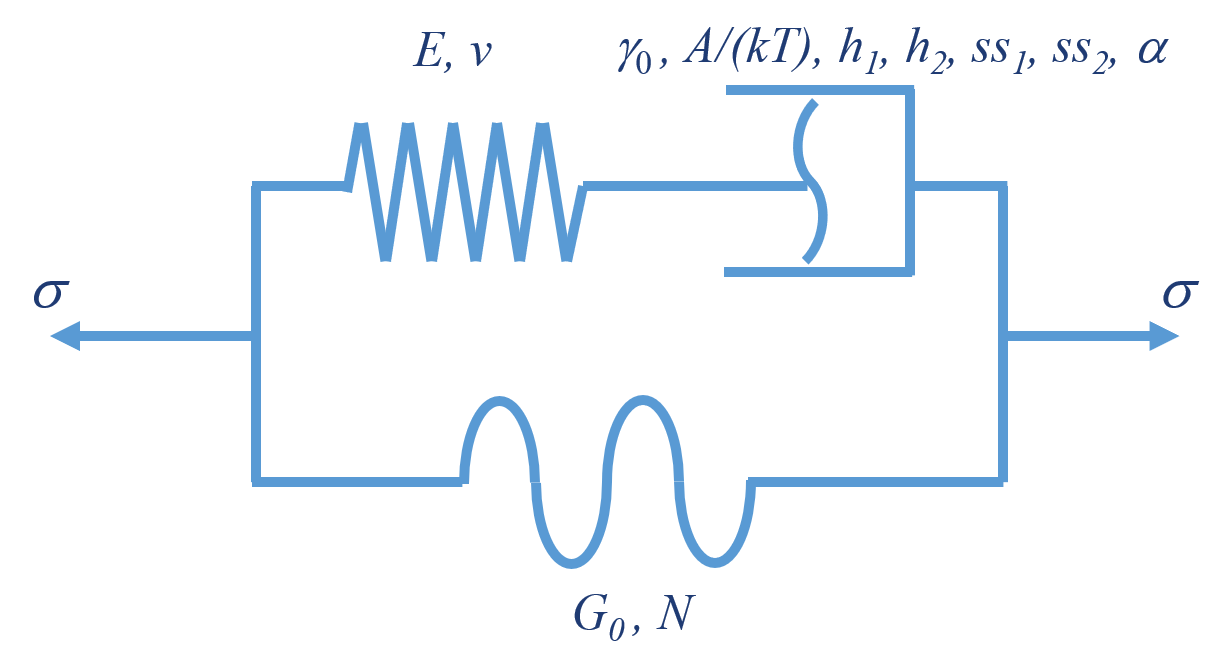 |
This advanded combined module integrates the thermal complementary module to achieve full thermo-mechanical coupling.
With this thermal component, heat transfer analysis can be conducted by considering heat generated from dissipation energy of the mechanical part.
Thermal softening effect under high strain rates can be captured accordingly. This module constitutive model captures the response of thermosets polymers such as Epoxy.
|
CExplicitSCP
CConstThermal
CSpringLinear
CDashpotGeneralized
CSpringLangevin
CElastoPlastic
|


|
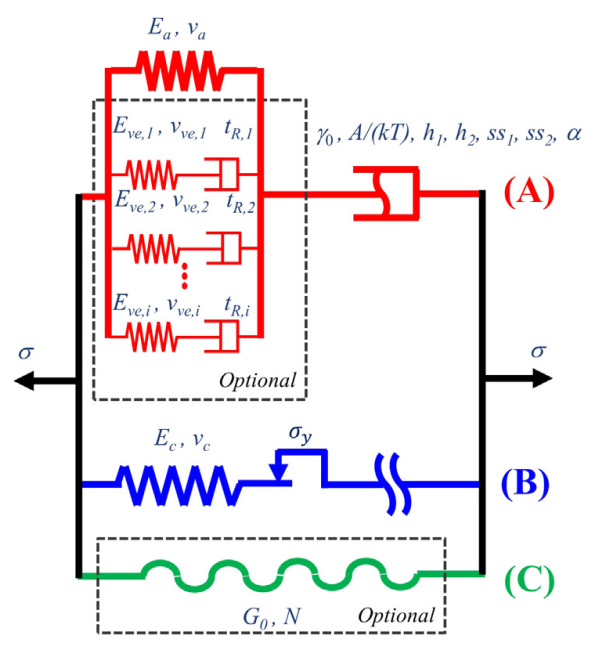 |
This advanced module combination describes the thermo-mechancial response of Semi-Crystalline Polymers (SCP) such as PA6, nylon 101 or PE.
The crystalline phase is explicitely described as an equivalent elastoplastic response that is activated according to the yield kinetics.
Apart from self-heating and thermal softening, this model captures very accurately the "Double Yield" phenomenon.
Reference: Int. J. Plast. 153 (2022) 103233 (General formulation, validation and applicability)
|
CUnifiedSCP
CConstThermal
CSpringLinear
CDashpotGeneralizedUnified
CSpringLangevin
|


|
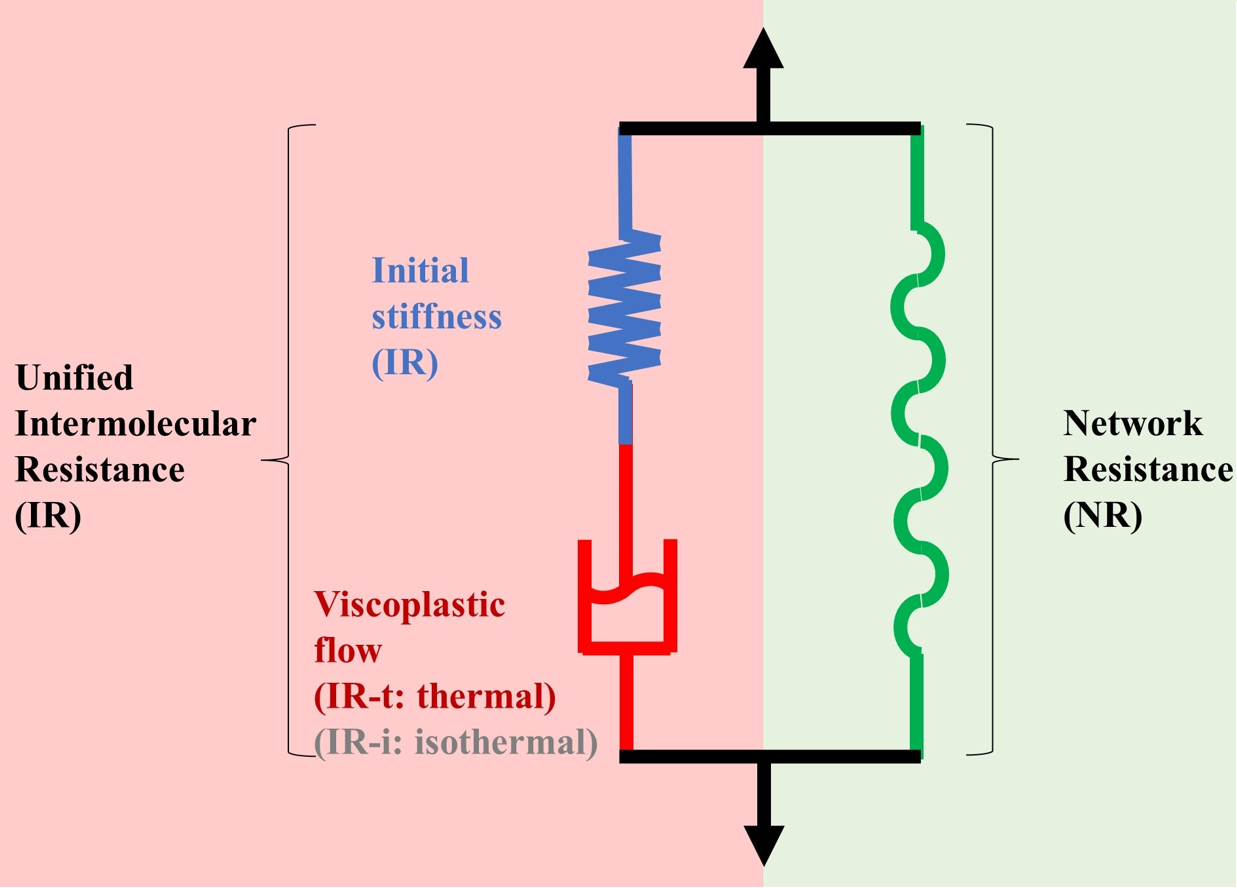 |
This module relies on a unified formulation to capture the thermo-mechanical response of a wide variety of polymers.
It uses a single viscoplastic law integrating both amorphous and crystalline phases under non-isothermal conditions useful to model either thermoplastics or thermosets.
Dependencies of temperature, strain rate and crystallinity on the material response can be studied with this module.
Apart from its accurary and applicability range, this module needs only three crystalline-related parameters with clear interpretation from stress–strain curves.
This unified model accurately predicts the experimental behavior of various plastics — including epoxy, PEEK, PES, PPS, PP, PET, PS, nylon 101, PA6, LDPE, HDPE — and their blends.
Reference1: Int. J. Plast. 159 (2022) 103469 (General formulation, validation and applicability)
Reference2: Mater. Des. 224 (2022) 111367 (Validation and applicability in quasistatic-to-dynamic regime)
Reference3: Polymers 15(5) (2023) (Application to multiscale modelling of UD composites under high speed compression)
Reference4: Polymers 16(8) (2024) (Application to characterization and modeling of recycled polyolefin blends)
Reference5: "Advanced characterization and thermomechanical modeling of PP/PE blends for innovations in recycled composites", 21st European Conference on Composite Materials (vol.2, p.576-582, 2024, ISBN:9782912985019)
Reference6: Polymers 17(9) (2025) (Mechanical strength predictions of UD composites using as matrix recycled PES/PEEK, PPS/PEEK and HDPE/PP blends) 
|
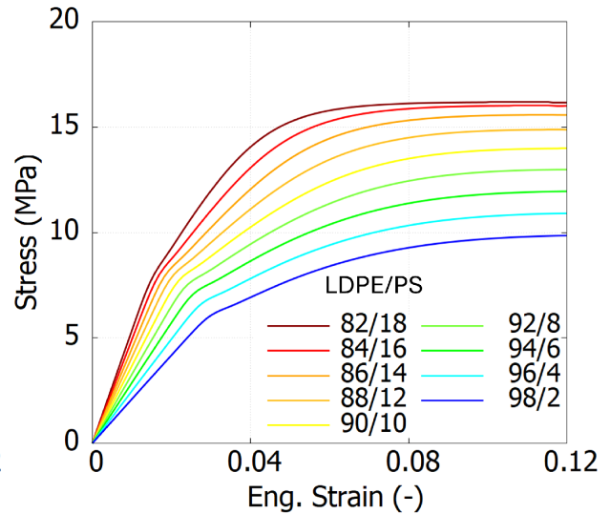
CUnifiedSCPNeuralNetwork 
C<Model>NeuralNetwork
CUnifiedSCP
CSpringLinear
|

|
 |
This module uses the Hybrid NN-based approach taking as input the Unified Semi-Crystalline Polymer model adapted for polymer blends.
This module predicts how varying polymer blend ratios influence stress–strain behavior, helping to address the challenge of cross-contamination caused by the difficulty in separating polymers during recycling.
Reference: Polymers 17(7) (2025) (Prediction mechanical behavior of LLDPE/PET, LLDPE/PA6 and LDPE/PS blends as a function of weight ratios). This paper was featured on the cover of Polymers, Issue 17, highlighting its significance within the field. (click here)
|